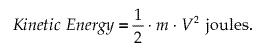if m be the indefinite but large mass flow in the wind, and actuator disk is placed
m perpendicular to the flow direction of wind, exerts a finite axial force is Dax, in this picture below no external force acts on the flow, so momentum is conserved and the flow does not expand further.
The velocity change obtained from the momentum relation is connected to the change of the kinetic power in the wind, by use this formula
at this is the formula that use to describe change of the kinetic power in the flow due to the axial force when the outer flow is included
Where :
A(delta)P is : the change of the kinetic power in the flow in the stream tube when it crosses the actuator disk
m : large mass flow in the wind
U : is velocity of wind until little past actuator boundary (see picture above)
V : is velocity of wind after fake boundary (see pincture)
Dax : Finite axial force
a : constant value from dynamic pressure function is 16/27 or 1/3
e : is fraction flows trough the stream tube
Betz limit is defined as the maximum fraction of the power in the wind that can theoretically be extracted, usually given as 16/27. or by other words that the maximum value for the power extracted from the wind is 0,59 or 16/27 of the total power in the wind.
An airstream moving through a turbine rotor disc cannot give up all of its energy to the blades because some kinetic energy must be retained in order to move the airstream away from the disc area after interaction. In addition there are frictional effects, which produce heat losses. Thus, a turbine rotor will never extract 100% of the wind's energy. 
As the air stream interacts with the rotor disc and power is extracted, the air stream speed is reduced by an amount described by the axial interference factor, a. This is the ratio of the upstream to the downstream wind speed. Equation below show the power using the axial interference factor.
by substitution, the power co-efficient Cp may be defined 
By differentiating with respect to a, the maximum value of Cp occurs when a = 0.33. so we can find that, Cp,max = 16/27 = 0.593 Cp,max = 16/27 = 0.593
this known as Betz limit,
The purpose of a wind turbine is to extract kinetic energy from the wind and convert this firstly to mechanical energy and then usually to electrical energy.
he Wind Turbine Power Equation is one of the most important equations a beginning wind enthusiast should memorize.
HWP = 0.5 x 1.23 x SA x WV3 x 0.25
(HWP) Harvestable Wind Power (w/hr) = 0.5 x AD (air density kg/cu m) x SA (sweep area m^2) x WV^3 (wind velocity m/s) x cP (coefficient of performance Betz limit 59.26%, R^1 or Copper loss, linear power curve to cubic curve matching — 0.25 for most systems)
Conversions:
1 square foot = 0.09290304 square meters
1 mile per hour = 0.44704 meters per second
1 kilometer per hour = 0.277777778 meters per second
Equation for a HAWT with 17′ diameter blades in 10mph wind.
17′ Diameter Blades (21.07m2 ), 10mph average wind (4.47m/s)
HWP = 0.5 x 1.23 x 21.07 x 89.31 x 0.25
WPH = 289Wh
Detail in Related post
- Calculation of Wind Energy and Wind Power
- Estimating and calculating air density
- Determining Wind Power Density
To represent of Annual and Seasonal Variations we can use The Weibull distribution, The Weibull distribution has been found to give a good representation of the variation in hourly mean wind speed over a year at many typical sites. This distribution takes the form
where F(U) is the fraction of time for which the hourly mean wind speed exceeds U.
because k describes the variability about the mean, and c is related to the annual mean wind speed U, they have another relation like this formula 
which I(at those symbol like F or I) is the complete gamma function
since the mean wind speed is given by
those relation can be derived by consideration of the probability density function
we can make a relation using equation of energy kinetic, The kinetic energy in air of mass (M) ・moving with speed V is given by the following equation in SI units :
The power in moving air is the flow rate of kinetic energy per second Therefore:
Which :
P = mechanical power in the moving air
rho = air density, kg/m3
A = area swept by the rotor blades, m2
V = velocity of the air, m/s
then, the volumetric flow rate is A.V, the mass flow rate of the air in kilogramsper second is rho.A.V, and the power is given by the following:
Two potential wind sites are compared in terms of the specific wind power expressed in watts per square meter of area swept by the rotating blades. It is also referred to as the power density of the site, and is given by the following expression:
This is the power in the upstream wind. It varies linearly with the density of the air sweeping the blades, and with the cube of the wind speed.
The power output, P, from a wind turbine is given by the well-known equation 
where
rho(greek symbol) is the density of air (1:225 kg/m3 )
Cp is the power coefficient,
A is the rotor
P swept area
U ist he wind speed.
The density of air is rather low, 800 times less than that of water which powers hydro plant, and this leads directly to the large size of a wind turbine. Depending on the design wind speed chosen, a 1.5 MW wind turbine may have a rotor that is more than 60 m in diameter
The power coefficient describes that fraction of the power in the wind that may be converted by the turbine into mechanical work. It has a theoretical maximum value of 0.593 (the Betz limit) and rather lower peak values are achieved in practice
The power coefficient of a rotor varieswith the tip speed ratio (theratio of rotor tip speed to free wind speed) and is only a maximum for a unique tip speed ratio. Incremental improvements in the power coefficient are continually being sought by detailed design changes of the rotor and, by operating at variable speed, it is possible to maintain the maximum power coefficient over a range of wind speeds. However, these measures will give only a modest increase in the power output. Major increases in the output power can only be achieved by increasing the swept area of the rotor or by locating the wind turbines on sites with higher windspeeds.
