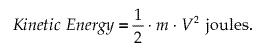if m be the indefinite but large mass flow in the wind, and actuator disk is placed
m perpendicular to the flow direction of wind, exerts a finite axial force is Dax, in this picture below no external force acts on the flow, so momentum is conserved and the flow does not expand further.



The velocity change obtained from the momentum relation is connected to the change of the kinetic power in the wind, by use this formula
at this is the formula that use to describe change of the kinetic power in the flow due to the axial force when the outer flow is included



Where :
A(delta)P is : the change of the kinetic power in the flow in the stream tube when it crosses the actuator disk
m : large mass flow in the wind
U : is velocity of wind until little past actuator boundary (see picture above)
V : is velocity of wind after fake boundary (see pincture)
Dax : Finite axial force
a : constant value from dynamic pressure function is 16/27 or 1/3
e : is fraction flows trough the stream tube

Betz limit is defined as the maximum fraction of the power in the wind that can theoretically be extracted, usually given as 16/27. or by other words that the maximum value for the power extracted from the wind is 0,59 or 16/27 of the total power in the wind.

An airstream moving through a turbine rotor disc cannot give up all of its energy to the blades because some kinetic energy must be retained in order to move the airstream away from the disc area after interaction. In addition there are frictional effects, which produce heat losses. Thus, a turbine rotor will never extract 100% of the wind's energy.



As the air stream interacts with the rotor disc and power is extracted, the air stream speed is reduced by an amount described by the axial interference factor, a. This is the ratio of the upstream to the downstream wind speed. Equation below show the power using the axial interference factor.



by substitution, the power co-efficient Cp may be defined


By differentiating with respect to a, the maximum value of Cp occurs when a = 0.33. so we can find that, Cp,max = 16/27 = 0.593 Cp,max = 16/27 = 0.593

this known as Betz limit,

The purpose of a wind turbine is to extract kinetic energy from the wind and convert this firstly to mechanical energy and then usually to electrical energy.
he Wind Turbine Power Equation is one of the most important equations a beginning wind enthusiast should memorize.

HWP = 0.5 x 1.23 x SA x WV3 x 0.25

(HWP) Harvestable Wind Power (w/hr) = 0.5 x AD (air density kg/cu m) x SA (sweep area m^2) x WV^3 (wind velocity m/s) x cP (coefficient of performance Betz limit 59.26%, R^1 or Copper loss, linear power curve to cubic curve matching — 0.25 for most systems)

Conversions:

1 square foot = 0.09290304 square meters
1 mile per hour = 0.44704 meters per second
1 kilometer per hour = 0.277777778 meters per second

Equation for a HAWT with 17′ diameter blades in 10mph wind.

17′ Diameter Blades (21.07m2 ), 10mph average wind (4.47m/s)

HWP = 0.5 x 1.23 x 21.07 x 89.31 x 0.25

WPH = 289Wh

Detail in Related post
- Calculation of Wind Energy and Wind Power

- Estimating and calculating air density

- Determining Wind Power Density

Aerodynamics of Horizontal-Axis Wind Turbines

To study the aerodynamics of wind turbines some knowledge of fluid dynamics in general is necessary and, in particular, aircraft aerodynamics, we can use Bernoulli theorem for steady, incom pressible flow is required together with the concept of continuity, and then use The Biot亡avart law, which will be familiar to those with a knowledge of electric and magnetic fields, is used to determine velocities induced by vortices


Aerodynamics of Horizontal-Axis Wind Turbines



As the air passes through the rotor disc, by design, there is a drop in static pressure such that, on leaving, the air is below the atmospheric pressure level. The air then proceeds downstream with reduced speed and static pressure ・this region
of the flow is called the wake. Eventually, far downstream, the static pressure in the wake must return to the atmospheric level for equilibrium to be achieved. The rise in static pressure is at the expense of the kinetic energy and so causes a further slowing down of the wind. Thus, between the far upstream and far wake conditions, no changein static pressure exists but there is a reduction in kinetic energy.

To represent of Annual and Seasonal Variations we can use The Weibull distribution, The Weibull distribution has been found to give a good representation of the variation in hourly mean wind speed over a year at many typical sites. This distribution takes the form

where F(U) is the fraction of time for which the hourly mean wind speed exceeds U.

because k describes the variability about the mean, and c is related to the annual mean wind speed U, they have another relation like this formula

which I(at those symbol like F or I) is the complete gamma function

since the mean wind speed is given by

those relation can be derived by consideration of the probability density function

Geographical Variationin the Wind Resource
Long-term Wind speed Variations

There is evidence that the wind speed at any particular location may be subject to very slow long-term variations. Although the availability of accurate historical records is a limitation, careful analysis by, for example, Palutikoff, Guo and Halliday (1991) has demonstrated clear trends. Clearly these may be linked to longterm temperature variations for which there is ample historical evidence. There is also much debate at present about the likely effects of global warming, caused by human activity, on climate, and this will undoubtedly affect wind climates in the coming decades.

Apart from these long-term trends there may be considerable changes in windiness at a given location from one year to the next. These changes have many causes.
They may be coupled to global climate phenomema such as el nino, changes in atmospheric particulates resulting from volcanic eruptions, and sunspot activity, to name a few. These changes add significantly to the uncertainty in predicting the energy output of a wind farm at a particular location during its projected lifetime.

we can make a relation using equation of energy kinetic, The kinetic energy in air of mass (M) ・moving with speed V is given by the following equation in SI units :



The power in moving air is the flow rate of kinetic energy per second Therefore:


Which :

P = mechanical power in the moving air
rho = air density, kg/m3
A = area swept by the rotor blades, m2
V = velocity of the air, m/s
then, the volumetric flow rate is A.V, the mass flow rate of the air in kilogramsper second is rho.A.V, and the power is given by the following:



Two potential wind sites are compared in terms of the specific wind power expressed in watts per square meter of area swept by the rotating blades. It is also referred to as the power density of the site, and is given by the following expression:

This is the power in the upstream wind. It varies linearly with the density of the air sweeping the blades, and with the cube of the wind speed.

Improved turbine designs and plant utilization have contributed to a decline in large-scale wind energy generation costs from 35 cents per kWh in 1980 to less than 5 cents per kWh in 1997 in favorable locations . At this price, wind energy has become one of the least-cost power sources. Major factors that have accelerated the wind-power technology development are as follows:

1. high-strength fiber composites for constructing large low-cost blades.
2. falling prices of the power electronics.
3. variable-speed operation of electrical generators to capture maxi mum energy.
4. improved plant operation, pushing the availability up to 95 percent.
5. economy of scale, as the turbines and plants are getting larger in size.
6. accumulated field experience (the learning curve effect) improvingthe capacity factor.

picture below show the construction of Modern wind turbine for utility scale power generation

The power output, P, from a wind turbine is given by the well-known equation



where
rho(greek symbol) is the density of air (1:225 kg/m3 )
Cp is the power coefficient,
A is the rotor
P swept area
U ist he wind speed.

The density of air is rather low, 800 times less than that of water which powers hydro plant, and this leads directly to the large size of a wind turbine. Depending on the design wind speed chosen, a 1.5 MW wind turbine may have a rotor that is more than 60 m in diameter

The power coefficient describes that fraction of the power in the wind that may be converted by the turbine into mechanical work. It has a theoretical maximum value of 0.593 (the Betz limit) and rather lower peak values are achieved in practice

The power coefficient of a rotor varieswith the tip speed ratio (theratio of rotor tip speed to free wind speed) and is only a maximum for a unique tip speed ratio. Incremental improvements in the power coefficient are continually being sought by detailed design changes of the rotor and, by operating at variable speed, it is possible to maintain the maximum power coefficient over a range of wind speeds. However, these measures will give only a modest increase in the power output. Major increases in the output power can only be achieved by increasing the swept area of the rotor or by locating the wind turbines on sites with higher windspeeds.

Geographical Variation in the Wind Resource


Ultimately the winds are driven almost entirely by the sun’s energy, causing differ ensential surface heating .The heating is most intense on land masses closer to the equator,and obviously the greatest heating occurs in the daytime, which means that the region of greatest heating moves around the earth’s surface as it spins on its axis. Warm air rises and circulates in the atmosphere to sink back to the surface in cooler areas. The resulting large-scale motion of the air is strongly influenced by coriolis forces due to the earth’s rotation. The result is a large-scale global circulation pattern. Certain identifiable features of this such as the trade winds and the ‘roaring forties’ are well known. The non-uniformity of the earth’s surface, with its pattern of land masses and oceans, ensures that this global circulation pattern is disturbed by smaller cal variations on continental scales. These ariations interact in a highly complex and non linear fashion to produce a somewhat chaotic result, which is at the root of the day to day unpredictability of the weather in particular locations. Clearly though, underlying tendencies remain which lead to clear climatic differences between regions.


These differences are tempered by more local topographical and thermal effects.Hill sand mountains result in local regions of increased wind speed. This is partly a result of altitude the earth’s boundary layer means that wind speed generally increases with height above ground, and hill tops and mountain peaks may' project into the higher wind-speed layers. It is also partly a result of the acceleration of the wind flow over and around hills and mountains, and funneling through passes or along valleys aligned with the flow. Equally, topography may produce areas of reduced wind speed, such as sheltered valleys, areas in the lee of a mountain ridge or where the flow patterns result in stagnation points.

If all of landscape geographic consisted of flat and smooth land, there would be little wind variation from place to place. But with the addition of hills, valleys, river bluffs and lakes,a complex and highly variable wind regime is created. Trees and buildings add to the complexity of the wind on a smaller scale. Each geographical feature influences wind flow in certain ways, as detailed below

Hills, plateaus and bluffs provide high ground on which to raise a wind turbine into a region of higher wind speeds. Valleys, which are lower and heltered, generally have lower wind speeds. However, all valleys are not necessarily poor wind sites. When oriented parallel to the wind flow, valleys may channel and improve the wind resource. A constriction to the valley may further enhance wind flow by funneling the air through a smaller area. This is often the case in narrow mountain passes or gaps that face the wind.

Valleys often experience calm conditions at night even when adjacent hilltops are windy. Cool, heavy air drains from the hillsides and collects in the valleys. The resulting layer of cool air is removed from the general wind flow above it to produce the calm conditions in the lowlands. Because of this, a wind turbine located on a hill may produce power all night, while one located at a lower elevation stands idle. This phenomenon is more likely to occur on high terrain features that reach at least several hundred feet above the surrounding land.

High terrain features can accelerate the flow of wind. An approaching air mass is often squeezed into a thinner layer so it speeds up as it crosses the summit. Over a ridge, maximum acceleration occurs when the wind blows perpendicular to the ridge line. Isolated hills and mountains may accelerate the wind less than ridges because more of the air tends to flow around the sides. The downward, or "lee," side of high terrain features should be avoided because of the presence of high wind turbulence.



Land areas adjacent to large bodies of water may be good wind sites for two reasons. First, a water surface is much smoother than a land surface, so air flowing over water encounters little friction. The best shoreline site is one where the prevailing wind direction is "on-shore." Second, when regional winds are light, as on a sunny summer day, local winds known as sea or lake breezes can develop because the land and water surfaces heat up at different rates.Because land heats more quickly than water, the warm rising air over the land is replaced by the cooler air from over the water. This produces an on-shore breeze of typically 8 to 12 mph or more. At night the breeze stops or reverses direction, as the land cools more quickly

Source :
http://www.energy.iastate.edu
Wind energy handbook,1987

History of Wind Energy

Wind is simple air in motion. It is caused by the uneven heating of the earth’s surface by the sun. Since the earth’s surface is made of very different types of land and water, it absorbs the sun’s heat at different rates. Since ancient times, people have harnessed the winds energy.

Over 5,000 years ago, the ancient Egyptians used wind to sail ships on the Nile River. Later, people built windmills to grind wheat and other grains. The earliest known windmills were in Persia (Iran). These early windmills looked like large paddle wheels. Centuries later, the people of Holland improved the basic design of the indmill. They gave it propeller-type blades, still made with sails. Holland is famous for its windmills. During the day, the air above the land heats up more quickly than the air over water.

The warm air over the land expands and rises, and the heavier, cooler air rushes in to take its place, creating winds. At night, the winds are reversed because the air cools more rapidly over land than over water. In the same way, the large atmospheric winds that circle the earth are created because the land near the earth's equator is heated more by the sun than the land near the North and South Poles. Today, wind energy is mainly used to generate electricity. Wind is called a renewable energy ource because the wind will blow as long as the sun shines.


Wind power is the conversion of wind energy into more useful forms, usually electricity using wind turbines. At the end of 2006, worldwide capacity of wind-powered generators was 74,223 megawatts; although it currently produces less than 1% of world-wide electricity use, it accounts for approximately 18% of electricity use in Denmark, 9% in Spain, and 7% in Germany. Globally, wind power generation more than quadrupled between 2000 and 2006.

Most modern wind power is generated in the form of electricity by converting the rotation of turbine blades into electrical current by means of an electrical generator. In windmills (a much older technology) wind energy is used to turn mechanical machinery to do physical work, like crushing grain or pumping water.

Wind power is used in
large scale wind farms for national electrical grids as well as in small individual turbines for providing electricity to rural residences or grid-isolated locations. Wind energy is ample, renewable, widely distributed, clean, and mitigates the greenhouse effect if used to replace fossil-fuel-derived electricity.

Windmills

Windmills have been used for at least 3000 years, mainly for grinding grain or pumping water, while in sailing ships the wind has been an essential source of power for even longer. From as early as the thirteenth century, horizontal-axis windmills were an integral part of the rural economy and only fell into disuse with the advent of cheap fossil-fuelled engines and then the spread of rural electrification. The use of windmills (or wind turbines) to generate electricity can be traced back to the late nineteenth century with the 12 kW DC windmill generator constructed by Brush in the USA and the research undertaken by LaCour in Denmark. However, for much of the twentieth century there was little interest in using wind energy other than for battery charging for remote dwellings and these low-power systems were quickly replaced once access to the electricity grid became available. One notable exception was the 1250 kW Smith–Putnam wind turbine constructed in the USA in 1941. This remarkable machine had a steel rotor 53 m in diameter, full-span pitch control and flapping blades to reduce loads. Although a blade spar failed catastrophically in 1945, it remained the largest wind turbine constructed forsome 40 years (Putnam, 1948).

Image from http://ec.europa.eu/research/energy

Golding (1955) and hepherd and Divone in Spera (1994) provide a fascinating history of early wind turbine development. They record the 100 kW 30 m diameter Balaclava wind turbine in the then USSR in 1931 and the Andrea Enfield 100 kW 24 m diameter pneumatic design constructed in the UK in the early 1950s. In this turbine hollow blades,open at the tip, were used to draw air up through the tower where another turbine drove the generator. In Denmark the 200 kW 24 m diameter ´ Gedser machine was built in 1956 while Electricite de France tested a 1.1 MW 35 m diameter turbine in 1963.
In Germany, Professor Hutter constructed a number of innovative, lightweight turbines in the 1950s and 1960s. In spite of these technical advances and the enthusiasm, among others, of Golding at the Electrical Research Association in the UK there was little sustained interest in wind generation until the price of oil rose dramatically in 1973.


The sudden increase in the price of oil stimulated a number of substantial Government-funded programmes of research, development and demonstration. In the USA this led to the construction of a series of prototype turbines starting with the 38 m diameter 100 kW Mod-0 in 1975 and culminating in the 97.5 m diameter 2.5 MW Mod-5B in 1987. Similar programmes were pursued in the UK, Germany and Sweden. There was considerable uncertainty as to which architecture might prove most cost-effective and several innovative concepts were investigated at full scale. In Canada, a 4 MW vertical-axis Darrieus wind turbine was constructed and this concept was also investigated in the 34 m diameter Sandia Vertical Axis Test.

In the UK, an alternative vertical-axis design using straight blades to give an ‘H’ type rotor was proposed by Dr Peter Musgrove and a 500 kW prototype constructed. In 1981 an innovative horizontal-axis 3 MW wind turbine was built and tested in the USA. This used hydraulic transmission and, as an alternative to a yaw drive, the entire structure was orientated into the wind. The best choice for the number of blades remained unclear for some while and large turbines were constructed with one, two or
three blades.

Source :
http://en.wikipedia.org
http://www.eia.doe.gov
http://ec.europa.eu/research/energy